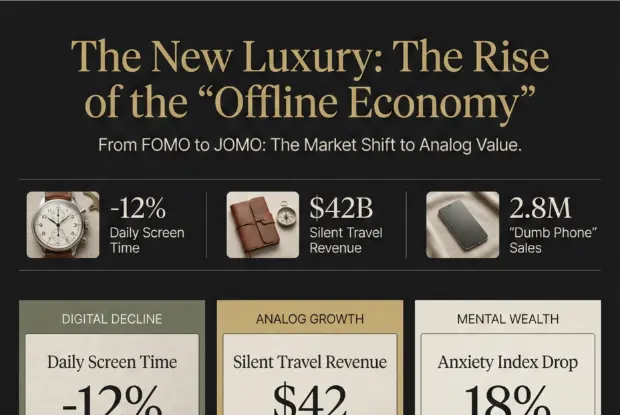
The Fact Behind Binary
Why Physics, Not Math, Rules Computing
- The Analog (Fragile): A waveform attempting to hold multiple distinct voltage levels (e.g., 0-9). It is jittery, susceptible to noise, and prone to 'drift.'
- The Binary (Robust): A square wave with only two states: High (On) and Low (Off). It ignores minor fluctuations, locking into stability via a wide threshold.
- The Threshold (Safety): The wide 'No Man's Land' between High and Low. This safety margin allows the signal to degrade without breaking the information.

Visual Intelligence by FactsFigs.com
Claude Shannon / Bell Labs / Engineering Physics
Data Source: Bell Labs
Overview
Almost every digital device around you runs on just two numbers: zero and one. But why only two? Binary is often described as a clever human invention, but in reality, it exists because of physical limits.
At a physical level, systems prefer stable states. Using more states might sound efficient, but more states mean more errors. Binary allows machines to be fast, cheap, and reliable. That trade-off alone is why it dominates computing.
State Stability
Systems prefer stable states (On/Off) because they naturally resist physical interference like heat and electrical noise.
Fast Facts
- The Benefit High 100 Binary signals can tolerate significant voltage fluctuation (noise) before a '1' is mistaken for a '0'.
- The Math 2^ 32 Bits The exponential growth of information density. 1 bit = 2 states; 32 bits = 4.2 billion states.
- The Scale 1 Trillion/s Modern processors switch states trillions of times per second. Only a binary system is robust enough to do this without crashing.
- The Failure High 100 Risk In multi-level systems, a signal meant to be a '7' can easily drift to an '8' due to minor heat changes.
The Physics of Noise (Why Not Base-10?)
When engineers design machines, they start with physics. In the real world, 'perfect' does not exist. Wires get hot, voltage fluctuates, and electrical interference is everywhere. If a computer tried to use 10 voltage levels (0-9), a tiny spike in heat could make a '7' drift into an '8.' The system would be fragile. Binary solves this by creating a massive safety margin. A signal can get messy, but as long as it stays above a certain threshold, it is still a '1.'
The Power of Exponents (Math from Physics)
A single bit is boring. But binary becomes useful when bits are combined. This growth is not linear; it is exponential. One bit is 2 states. Two bits are 4. By the time you reach 32 bits, you have over 4 billion distinct possibilities. We trade the complexity of the signal (keeping it simple) for the complexity of the quantity (using billions of them). This is how simple on/off signals scale into 4K video and AI.
Surviving Scale (Reliability)
Binary doesn't just work; it scales. It makes errors detectable and correctable. Because there are only two valid states, illegal states are easy to spot. This reliability allows modern computing to exist at scale. Data centers process billions of signals every second. If those systems relied on fragile analog states, they would collapse under their own complexity. Binary keeps them stable.
Conclusion
Binary is not a limitation of imagination; it is a response to reality.
It persists because in the physical universe, stable states are easier to maintain than precise ones. We built our digital empire on 0 and 1 because reliability matters more than elegance.
Data Source and Attribution
Bell LabsIEEE SpectrumComputer History Museum
This analysis relies on fundamental principles of electrical engineering and information theory, specifically Claude Shannon's 'A Mathematical Theory of Communication' and standard Signal-to-Noise Ratio (SNR) physics.
Disclaimer: This content explains the fundamental engineering principles behind digital logic systems.
Visual generated via CodePLU AI Engine (v1.0).
2026-02-06